Версия для печати
Вернуться к списку

Нарушение закона физики

Упругие свойства материалов интересовали человечество с древнейших времен. Существенный прогресс в понимании упругости был достигнут в работах Роберта Гука, английского исследователя, работавшего во второй половине XVII века. Считается, что наряду с Исааком Ньютоном Гук «ответственен» за закон всемирного тяготения.

В теории упругости он известен открытием закона Гука, который гласит, что сила, которая требуется, чтобы растянуть материал (см. рисунок), оказывается пропорциональна величине растяжения. Коэффициент пропорциональности характеризует конкретный материал и называется объемным модулем Юнга. Для тонких пластин удобно работать с модулем Юнга Y, который получается умножением объемного модуля Юнга на толщину пластины. (Модуль Юнга в системе единиц СИ измеряется в ньютонах на метр (н/м).) Кроме растяжения или сжатия в плоскости у тонких пластин возникает возможность изгиба. Энергия, связанная с изгибом, определяется величиной изгибной жесткости. (В системе СИ изгибная жесткость измеряется в джоулях.)

Возникающий при уменьшении толщины пластины до одного атомарного слоя объект принято называть кристаллической мембраной. Самый известный пример — это графен, который представляет собой один слой атомов углерода, расположенных в узлах шестигранных (сотовых) ячеек. Графен был получен в лаборатории Андреем Геймом и Константином Новоселовым в 2004 году. За это открытие им обоим была присуждена Нобелевская премия по физике в 2010 году. В настоящее время графен находит широкое применение в различных областях, включая биомедицину (сенсоры молекул), химию (молекулярные фильтры) и электронику (графеновые конденсаторы и транзисторы). Часто можно встретить утверждение, что графен является очень прочным материалом. Это связано с тем, что его модуль Юнга равен 340 н/м. У одноатомного слоя алюминия модуль Юнга в 50 раз меньше! Графен также характеризуется достаточно большим значением изгибной жесткости, равным 1,6 на 10^–19 джоулей.

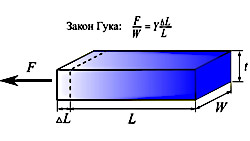
Брусок, к одному концу которого приложена растягивающая сила F. Эта сила приводит к продольному растяжению бруска. Модуль Юнга Y связан c объемным модулем Юнга E как Y=E t

Как известно из школьного курса физики, атомы в кристаллах совершают тепловые колебания около своих положений равновесия. Эти же тепловые колебания могут вызывать изгибные деформации мембраны. Можно оценить, как величина изгибных деформаций, вызванных тепловыми флуктуациями, растет с увеличением продольного размера мембраны, и найти, при каком размере она сравнивается с толщиной мембраны. Последняя для одноатомного слоя имеет порядок долей нанометра (нм). Соответствующая длина, называемая длиной Гинзбурга, оказывается для графена исключительно маленькой. Она равна 1 нм при комнатной температуре. Поэтому для всех исследуемых в лабораториях образцах графена тепловые изгибные флуктуации оказываются принципиально важны. Для сравнения можно оценить длину Гинзбурга для листа бумаги толщиной 1 мм. Она оказывается равной 1000 км при комнатной температуре! Именно поэтому в обычной жизни мы, как правило, не встречаемся с проявлением тепловых изгибных флуктуаций.

Несмотря на то что роль длины Гинзбурга в физике кристаллических мембран была осознана только в середине 1980-х годов, важность тепловых изгибных флуктуаций была понятна еще с 1930-х годов. В это время Лев Ландау и Рудольф Пайерлс, английский физик-теоретик, один из пионеров концепции дырочной проводимости в полупроводниках и теории экситонов, независимо друг от друга показали, что бесконечные кристаллические мембраны из-за тепловых изгибных флуктуаций должны разрушаться, превращаясь в бесформенный комок атомов. Другими словами, получается, что их результат, который до сих пор входит в стандартные учебники по теоретической физике, например, в курс Ландау и Лифшица, запрещает существование графена!

Как же примерить ставшее классическим утверждение Ландау—Пайерлса и чешуйки графена, имеющиеся в настоящее время во многих лабораториях мира. Как это обычно бывает для многих вопросов, разгадка скрыта в деталях. Обратим внимание на то, что, согласно результату Ландау—Пайерлса, не существует кристаллических мембран бесконечных размеров. При любой заданной температуре существует предельный продольный размер мембраны, когда изгибных тепловых флуктуаций недостаточно для разрушения мембраны. Подчеркнем, что этот размер не нужно путать с длиной Гинзбурга! Если оценить такой предельный размер для графена при комнатной температуре, то получится гигантская длина. Так как в лабораториях чешуйки графена обычно имеют размер всего несколько микрометров, то, казалось бы, разгадка найдена!

Как это часто бывает в физике, самое простое объяснение явления не всегда оказывается правильным. Утверждение Ландау—Пайерлса основано на предположении, что изгибные тепловые флуктуации не взаимодействуют друг с другом, как говорят, являются гармоническими. Оказывается, что для графена такая идеализация справедлива только для очень маленьких размеров, меньше длины Гинзбурга. Для графена микронного размера игнорировать взаимодействие изгибных флуктуаций между собой оказывается принципиально неправильным. Их взаимодействие приводит к тому, что изгибная жесткость мембраны начинает расти степенным образом с увеличением продольного размера, то есть чем больше размер мембраны, тем все труднее становится ее изогнуть. Этот эффект был теоретически предсказан в середине 80-х годов прошлого века. Он приводит к тому, что бесконечная кристаллическая мембрана оказывается устойчивой при температурах ниже некоторой критической. Для графена критическая температура оказывается выше 10 тыс. градусов Кельвина. Такая высокая критическая температура означает, что тепловые изгибные флуктуации никогда не разрушают графен, так как при таких высоких температурах уже расплавится кристаллическая решетка.

Взаимодействие изгибных флуктуаций приводит к ряду интересных явлений в кристаллических мембранах, которые называют термином аномальная упругость. В области малых продольных деформаций нарушается закон Гука: деформация мембраны как целого становится степенной функцией приложенной силы со значением показателя степени меньше единицы, который к тому же не зависит от типа атомов мембраны, то есть является универсальным. Линейный закон Гука восстанавливается только при достаточно больших значениях деформации. Недавно такой нелинейный закон Гука для графена был измерен экспериментально. Также у графена в широкой области параметров оказывается отрицательным коэффициент Пуассона. Напомним, что положительный коэффициент Пуассона характеризует, как при растяжении в одном направлении материал сжимается в поперечном направлении. У графена вместо сжатия в поперечном направлении происходит растяжение! Наконец, вплоть до ультранизких температур коэффициент теплового расширения графена оказывается отрицательным, то есть графен при нагреве сжимается, вместо того чтобы расширяться, как это делает большинство веществ.

В заключение можно сказать, что физика кристаллических мембран, в частности графена, в очередной раз подтверждает, что в настоящей науке не бывает абсолютных истин: все законы выводятся в рамках некоторых предположений, о которых не стоит забывать. В теории кристаллических мембран все еще осталось значительное количество вопросов, связанных с аномальной упругостью, требующих теоретического и экспериментального изучения. В частности, этим занимаются ученые из Физико-технического института им. А. Ф. Иоффе РАН, Института теоретической физики им. Л. Д. Ландау РАН и Сколковского института науки и технологий в рамках гранта РФФИ 20-52-12019.